D The Math Library
The Math Library allows high precision computations not available through standard integer operations. Floating Point (FP) numbers use decimal representation to express fractional quantities. This format also allows scientific notation to represent very large and very small numbers.
To enable floating point operations, an application must include a GEOS Math Library. There are two Math Libraries: math.h and math.goh. The file math.h includes what you need to get floating point numbers to work within your application. The object file, math.goh (which includes math.h), includes the float-format controller, an object that allows the user to control how floating point numbers are formatted within an application.
In most cases, the mere inclusion of the Math Library will eliminate the need to directly call Math Library routines. (The C compiler will parse the mathematical expressions into appropriate floating point routines.) You may, however, wish to call some of these routines directly. Developers using Object Assembly must use this latter approach. C developers may also want to directly manipulate the FP stack for involved computations that they would rather not leave to the compiler. This approach is discussed in the latter half of this chapter.
Use of math.goh is optional, depending on the purpose of the application. A spreadsheet application, for example, might want to allow the user to format FP numbers. Other applications might not want to include this file.
D.1 Basic Math Functions
The Math Library includes many routines and structures that make the manipulation of FP numbers possible. Most of these are transparent to a C programmer.
C includes the following floating point types: float, double, and long double. A floating point number in GEOS is of type FloatNum, which uses the IEEE 80 bit standard (equivalent to a long double) to represent floating point values. FloatNum has overloaded the float, double, long double, and all basic match functions.
A FloatNum consists of a one bit sign, a 15 bit exponent, and a 64 bit mantissa. The maximum exponent allowed is 7FFEh. An exponent of 7FFFh (FP_NAN) signals an underflow or overflow. You may check the value of this exponent using the macro FLOAT_EXPONENT to extract the exponent of a FloatNum.
Code Display D-1 Extracting an Exponent
FloatNum myNum;
if (FLOAT_EXPONENT((&myNum)) == FP_NAN)
{
return(ERROR);
}
If you use any floats, doubles, or long doubles in your application, GEOS will convert these types into FloatNum values automatically and call the appropriate GEOS functions to manipulate the numbers. As this is the case, it is usually easier to declare any floating point variables in your application as FloatNum types (or long doubles). This cuts down on conversion time.
The Math Library provides all the familiar mathematical functions to manipulate these GEOS FP numbers (addition, multiplication, computation of logarithms, etc.). In C, most of these functions will automatically be called when their corresponding C operation involving FP numbers take place. (For example, when using the `+’ binary operator to add two FP numbers, the Math Library will use the corresponding FloatAdd() routine.)
You may, under special circumstances, wish to use these math routines directly. If you do so, you will need to manipulate the floating point stack manually, pushing numbers on the stack and making sure numbers are in the proper stack location to perform each operation. In most cases, the FP math routines operate on numbers already in place on the FP stack; they take and return no arguments of their own.
Two functions you will need to use if you take this approach are FloatPushNumber() and FloatPopNumber(). FloatPushNumber() takes the address of a variable (of type FloatNum) to push onto the FP stack; FloatPopNumber() takes the address of a buffer to place an FP number popped off the FP stack. Other routines (for example, FloatAdd()) can then be called to operate on the FP stack. (See Code Display D-2 for an example using this approach.)
There are many other routines that perform stack manipulation by shifting locations of FP numbers on the stack (FloatRoll(), FloatDrop(), etc.). These routines are covered in detail in the latter part of this chapter because they are seldom needed in a C applications.
D.1.1 Algebraic Functions
Algebraic routines perform algebraic operations on FP numbers. The Math Library provides all of the basic algebraic routines that operate on GEOS FP numbers (addition, subtraction, etc.). The table in Table D-1 lists the function names and the operations they perform.
|Function |C Operation |Function | |:—————-|:———–|:——————————–| |FloatAdd() |+ |addition | |FloatSub() |- |subtraction | |FloatMultiply() |* |multiplication | |FloatDivide() |/ |division | |FloatDIV() |(int) (X/Y) |division returning integer result| |FloatMod() |X % Y |modulo | |FloatFactorial() | |factorial | |FloatNegate() |-X |negation | |FloatInverse() |1/X |inversion | |FloatAbs() |abs(X) |absolute value | |FloatMax() | |maximum of two numbers | |FloatMin() | |minimum of two numbers | |FloatLt0() |X < 0 |less than 0 | |FloatGt0() |X > 0 |greater than 0 | |FloatEq0() |X = 0 |equal to 0 | |FloatFrac() | |returns fractional portion of X | |FloatTrunc() | |truncates X to its integer value | |FloatInt() |(int) X |returns integer of X, rounded down| |FloatIntFrac() | |separates X into integer and fraction| |FloatRound() | |rounds X to a given decimal places| Table D-1 Basic FP Functions and corresponding C operations (if any)
If you wish to call these routines directly rather than rely on the C operations, you may manipulate the floating point stack directly. To add two numbers using FloatAdd() for example, you would use FloatPushNumber() twice to push the two values to add onto the FP stack, and then call FloatAdd() to operate on the FP stack. (See Code Display D-2.)
Code Display D-2 Adding Two FP Numbers
/*
* The following two methods each add two FP numbers and return the result. The
* first method is familiar C code. The second example uses the floating point
* routines from math.h directly. Note that the C code will be assembled into code
* that uses FloatAdd() also, but that this is transparent to the code.
*/
@method MyProcessClass, MSG_SUM_FLOATS {
long double number1, number2, number3;
number1 = 1.0;
number2 = 2.0;
number3 = number1 + number2;
return(number3);
}
@method MyProcessClass, MSG_SUM_FLOATS_MANUALLY {
long double number1, number2, number3;
number1 = 1.0;
number2 = 2.0;
FloatPushNumber(&number1); /* Push number1 onto the FP stack. */
FloatPushNumber(&number2); /* Push number2 onto the FP stack. */
FloatAdd(); /* Add the top two numbers on the FP stack. The
* result will be placed on top of the FP stack.*/
FloatPopNumber(&number3); /* Pop the result into the number3 variable. */
return(number3);
}
Algebraic routines included in the Math Library are listed in Table D-1. As can be seen in the table, several functions have no equivalent C operation. Consult “Direct FP Operations” for more details on using these functions.
D.1.2 Transcendental Functions
The Math Library provides an array of transcendental routines that operate on GEOS FP numbers. A transcendental function is one which cannot be derived through algebraic means. Examples of transcendental functions include the trigonometric functions (sine, cosine, etc.) and the logarithmic functions (log, natural log, etc.).
The table in Table 4-2 lists the function names and the operations they perform. Typical functions in C are listed alongside. (The basic language of C itself includes no such transcendental functions but almost all compilers include a C math library that does.) As can be seen in the table, several functions have no equivalent C operation. Consult “Float Formats” for more details on using these functions.
|Function |C Equivalent |Operation | |:—————–|:————–|:—————————-| |FloatSin() |sin() |sine | |FloatCos() |cos() |cosine | |FloatTan() |tan() |tangent | |FloatArcSin() |asin() |arc-sine (inverse sine) | |FloatArcCos() |acos() |arc-cosine (inverse cosine) | |FloatArcTan() |atan() |arc-tangent (inverse tangent)| |FloatArcTan2() | |arc-tangent given two coordinates| |FloatSinh() |sinh() |hyperbolic sine | |FloatCosh() |cosh() |hyperbolic cosine | |FloatTanh() |tanh() |hyperbolic tangent | |FloatArcSinh() |asinh() |hyperbolic arc-sine | |FloatArcCosh() |acosh() |hyperbolic arc-cosine | |FloatArcTanh() |atanh() |hyperbolic arc-tangent | |FloatExp() | |e raised to the power X | |FloatExponential()|exp() |X raised to the Y power | |FloatLg() | |logarithm to the base 2 | |FloatLog() |log() |logarithm to the base 10 | |FloatLn() | |logarithm to the base e (natural log)| |FloatLn1plusX() | |natural log of (1 + X) | |FloatSqr() | |square of X | |FloatSqrt() |sqrt() |square root | Table 4-2 Transcendental Floating Point Functions
D.1.3 Random Number Generation
FloatRandomize(), FloatRandom(), FloatRandomN()
The Math Library also provides routines to create random numbers. Using any of these routines requires that you manually push and pop numbers on the FP stack.
FloatRandomize() primes the random number generator, in preparation for a call to FloatRandom() or FloatRandomN(). If FloatRandomize() is passed the flag RGIF_USE_SEED, the routine must also pass a developer supplied seed.
FloatRandom() returns a random value between 0 (inclusive) and 1 (exclusive). The number is placed on top of the FP stack. To assign that value to a variable, use FloatPopNumber().
FloatRandomN() returns a random value between 0 (inclusive) and N (exclusive), where N is an integer. The integer value must be on top of the FP stack. The returned integer is pushed onto the FP stack.To assign that value to a variable, use FloatPopNumber().
Code Display D-3 Creating a Random Number
/*
* This method takes a passed seed (passedSeed) and returns a random integer
* between 0 and 100.
*/
@method MyProcessClass, MSG_GET_RANDOM_FLOAT {
long double randomX;
/* Prime the random number generator. */
FloatRandomize(RGIF_USE_SEED, passedSeed);
randomX = 100;
FloatPushNumber(&randomX);
FloatRandomN();
FloatPopNumber(&randomX);
return(randomX);
}
D.2 Conversions to Other Types
In many cases, FP numbers will need to be converted to different types for use in different parts of an application. For example, floating point numbers may be involved in a complex function that returns an integer. FP numbers may also need to appear to the user as ASCII text.
Converting Into Other Floats
There are several routines which convert GEOS FP numbers into other float formats, compatible with the C types float and double. Typically in C, this conversion is accomplished by casting the FP numbers into the other type. It is therefore done automatically for you.
If you are working in Assembly or you wish to directly pass floats or doubles to C stubs, consult “Direct FP Operations”.
Converting ASCII to FP Numbers
FloatAsciiToFloat()
FloatAsciiToFloat() converts a number represented in an ASCII text format into a FP number. The routine recognizes two flags:
-
FAF_PUSH_RESULT
Pushes the result onto the FP stack. -
FAF_STORE_NUMBER
Stores the result in a specified address.
The routine must also be passed a pointer to the string to convert, the number of characters in the string to convert (starting at the address) and the buffer to store the FP number if passing FAF_STORE_NUMBER.
Converting FP Numbers to ASCII
FloatFloatToAscii(), FloatFloatToAscii_StdFormat(), FloatFloatIEEE64ToAscii_StdFormat()
FloatFloatToAscii() converts an FP number into ASCII text format. The routine must be passed a stack frame, which may be set up by declaring a local variable of type FFA_stackFrame and moving data into the appropriate fields. You should also pass the routine a pointer to a buffer to store the resultant string.
The FFA_stackFrame is a union of two structures: FloatFloatAsciiData or FloatFloatToDateTimeData. You will want to use the FloatFloatToAsciiData structure in most cases; FloatFloatToAsciiDateTimeData is used to format a FP number (representing a date and time) into a date-time format passed in the structure. The routine checks a bit in the structure to see which structure is being passed.
D.2.0.1 Normal Conversions
The FloatFloatToAsciiData structure is used most often in formatting FP numbers into ASCII. The structure is rather large and cumbersome to set up. You may wish to use the routine FloatFloatToAscii_StdFormat() which sets up many of these entries automatically. (Code Display D-4 lists the entries of the FloatFloatToAsciiData structure.)
Code Display D-4 FloatFloatToAsciiData Structure
typedef struct {
/*
* FFA_params stores the entries that the caller must set up.
*/
FloatFloatToAsciiParams FFA_params;
/*
* These entries store information returned by FloatFloatToAscii() that may be
* examined.
*/
word FFA_startNumber;
word FFA_decimalPoint;
word FFA_endNumber;
word FFA_numChars;
word FFA_startExponent;
/*
* The rest of the entries are for internal use only.
*/
word FFA_bufSize;
word FFA_saveDI;
word FFA_numSign;
byte FFA_startSigCount;
byte FFA_sigCount;
byte FFA_noMoreSigInfo;
byte FFA_startDecCount;
byte FFA_decCount;
word FFA_decExponent;
word FFA_curExponent;
byte FFA_useCommas;
byte FFA_charsToComma;
char FFA_commaChar;
char FFA_decimalChar;
} FloatFloatToAsciiData;
FFA_params is a structure that stores the following entries of its own:
formatFlags
Flags specifying the look and feel of the ASCII text format (see below for allowed flags).
decimalOffset
Integer which specifies the number of decimal places to shift the output. For example, to display a number in terms of millions, a decimalOffset of -6 shifts the decimal point six places to the left; to display in terms of tenths would require a decimalOffset of 1.
totalDigits
Integer which specifies the maximum number of decimal places (integer and decimal portions) that the FP number may exhibit. The ASCII string is truncated if the length of the string is greater than this number.
decimalLimit
Integer which specifies the maximum number of digits to the right of the decimal point. For example a decimalLimit of 2 would print out 123.456789 as 123.46.
preNegative
Characters used to precede a negative number, in the format of a null terminated text string.
postNegative
Characters used to follow a negative number, in the format of a null terminated text string.
prePositive
Characters used to precede a positive number, in the format of a null terminated text string.
postPositive
Characters used to follow a positive number, in the format of a null terminated text string.
header
Characters used to precede the number, in the format of a null terminated text string. For example, a typical header for a currency format might be “$”.
trailer
Characters used to follow a FP number, in the format of a null terminated text string.
The formatFlags record is a record of type FloatFloatToAsciiFormatFlags and defines the format of the ASCII output. Set the appropriate flags to get the desired output.
-
FFAF_FROM_ADDR
Set if routine should take the FP number from a specified address, rather than the FP stack. This pointer (*number) should be passed to FloatFloatToAscii() if this flag is set. -
FFAF_DONT_USE_SCIENTIFIC
Set if the result should not be expressed in scientific notation under any condition. If this is set, the number will always be formatted in fixed format. -
FFAF_SCIENTIFIC
Set if the result should be expressed in scientific notation even if the number can be expressed in fixed point format. For example, the number `2’ will be expressed as “2 x 100.” -
FFAF_PERCENT
Set if the result should be expressed as a percentage. -
FFAF_USE_COMMAS
Set if the result should use commas to separate thousands. -
FFAF_NO_TRAIL_ZEROS
Set if extraneous zeros to the right of the decimal point should be ignored. For example, “123.67000000” will be reduced to “123.67.” -
FFAF_NO_LEAD_ZEROS
Set to ignore the lead zero for a number less than one. That is, “0.123” is reduced to “.123.” -
FFAF_HEADER_PRESENT
Set if a header is present; this speeds up conversion. -
FFAF_TRAILER_PRESENT
Set if a trailer is present; this speeds up conversion. -
FFAF_SIGN_CHAR_TO_FOLLOW_HEADER
Set if sign character(s) should follow the header. -
FFAF_SIGN_CHAR_TO_PRECEDE_TRAILER
Set if sign character(s) should precede the trailer.
The rest of the entries in FloatFloatToAsciiData store information filled in by FloatFloatToAscii(). These entries are described below:
FFA_startNumber stores the offset to the start of numeric characters in the ASCII buffer.
FFA_decimalPoint stores the offset to the decimal point character or zero if no decimal point is present.
FFA_endNumber stores the offset to the end of the numeric characters in the ASCII buffer.
FFA_numChars stores the total number of characters in the ASCII buffer (excluding the null terminator). This entry is set to zero if an error is encountered.
FFA_startExponent stores the offset to the “E” character in the ASCII buffer or zero if no exponent is present. Applications can check this to see if the number was expressed in scientific notation using the `E’ format.
D.2.0.2 Date-Time Conversions
FFA_stackFrame may contain FloatFloatToAsciiDateTimeData if FloatFloatToAscii() is being used to convert a FP number into a date-time format. In that case FFA_stackFrame contains the structure FloatFloatToDateTimeData instead of FloatFloatToAsciiData. (FFA_stackFrame is a union.)
FloatFloatToDateTimeData contains one entry, FFA_dateTimeParams. This structure contains several flags which specify how the date-time should be formatted and a number of entries which break down the date-time into its respective parts (year, month, day etc.) If none of these entries are filled in, the date-time is taken from the top of the FP stack.
Date-times are represented by FP numbers in GEOS. The integer portion represents dates as integers counted from Jan 1, 1900, which is designated as 1. The highest date allowed is 73050 (December 31, 2099). The fractional portion represents a fraction of the day between midnight (0.000000) and 11:59:59 p.m. (0.999988). This fractional value is derived from the hour, minute and second of the day.
Code Display D-5 DateTime Parameters
typedef struct {
FloatFloatToDateTimeFlags FFA_dateTimeFlags;
word FFA_year;
byte FFA_month;
byte FFA_day;
byte FFA_weekday;
byte FFA_hours;
byte FFA_minutes;
byte FFA_seconds;
} FloatFloatToDateTimeParams;
/*
* FloatFloatToDateTimeFlags record
*/
typedef WordFlags FloatFloatToDateTimeFlags;
#define FFDT_DATE_TIME_OP 0x8000
#define FFDT_FROM_ADDR 0x4000
#define FFDT_FORMAT 0x3fff
The flag FFDT_DATE_TIME_OP is set to notify the FloatFloatToAscii() routine that this operation is a date-time format, not a normal float to ASCII conversion. This flag must be set if you want to convert the FP number into a date-time format using FloatFloatToAscii().
FFDT_FROM_ADDR is set if the date-time FP number should not be taken from the FP stack (or passed directly in the FloatFloatToDateTimeParams structure) but should instead be taken from the address passed in FloatFloatToAscii().
FFDT_FORMAT stores the DateTimeFormat that the routine will use to format the number into a date-time string.
If the date-time is directly passed in, and not taken from an FP date-time number either at a passed address or the top of an FP stack, FloatFloatToAscii() looks at the other passed parameters.
FFA_year specifies the year. The value must be between 1900 and 2099. This is not a one-based year, as it is when presented as a date-time number.
FFA_month is the month of the year, a value between 1 and 12.
FFA_day is the day of a month, a value between 1 and 31.
FFA_hour specifies the hour of the day, a value between 0 and 23. Zero specifies midnight.
FFA_minutes specifies the minute of the hour, a value between 0 and 59.
FFA_seconds specifies the second of the minute, a value between 0 and 59.
D.2.0.3 Using Standard Formats
FloatFloatToAscii_StdFormat() uses a pre-set stack frame, eliminating the need to set up the variables of the FloatFloatToAsciiData structure manually. The only flags recognized are FFAF_FROM_ADDR, FFAF_SCIENTIFIC, FFAF_PERCENT, FFAF_USE_COMMAS, and FFAF_NO_TRAIL_ZEROS. The developer must pass the number of total digits and the number of decimal digits desired. If the flag FFAF_FROM_ADDR is used, a pointer to a FP number (not on the FP stack) must also be passed.
The standard format sets the following elements of the stack frame to zero: decimalOffset, header, trailer, postNegative, prePositive, and postPositive. The structure element preNegative is set to the minus sign (“-“).
FloatFloatIEEE64ToAscii_StdFormat() performs the same operation as FloatFloatToAscii_StdFormat() except that the FP number is passed (in 64 bit format) and is not taken from the stack. The entire FP number (not just a pointer to it) must be passed. All criteria for FloatFloatToAscii_StdFormat() applies to this routine, except that the flag FFAF_FROM_ADDR is not used.
D.2.0.4 Date and Time Routines
FloatGetDateNumber(), FloatDateNumberGetYear(), FloatDateNumberGetMonthAndDay(), FloatDateNumberGetWeekday(), FloatGetTimeNumber(), FloatTimeNumberGetHour(), FloatTimeNumberGetMinutes(), FloatTimeNumberGetSeconds()
FloatGetDateNumber(), when passed the month, day, and year, converts the data into an FP “date number” representation. This format represents dates as integers counted from Jan 1, 1900, which is designated as 1. The highest date allowed is 73050 (December 31, 2099).
FloatDateNumberGetYear(), FloatDateNumberGetMonthAndDay() and FloatDateNumberGetWeekday() all return the appropriate data, either the year, month and day, or weekday, given an FP “date number” as defined above. All data are returned as integers, not as FP numbers, and the original FP “date number” is popped off of the stack. Years are returned as integers between 1900 and 2099. Month and Days are returned as integers between 1 and 12, and 1 and 31, respectively. Weekdays are returned as integers between 1 and 7, where 1 is Sunday, 2 is Monday, etc.
FloatGetTimeNumber() when passed hours, minutes, and seconds returns an FP decimal representation between midnight (0.000000) and 11:59:59 p.m. (0.999988).
FloatTimeNumberGetHour(), FloatTimeNumberGetMinutes() and FloatTimeNumberGetSeconds() return the appropriate data given an FP “time number” as defined above. The original FP “time number” is popped off of the stack.
Note that both “date numbers” and “time numbers” can be added to specify a specific point in time. For example, 73050.999988 would specify December 31, 2099, 11:59:59. Since these formats are in FP format, they can be operated on with all standard functions in the FP library.
D.2.0.5 Miscellaneous Date Time Routines
FloatGetDaysInMonth(), FloatGetNumDigitsInIntegerPart(), FloatFormatNumber()
FloatGetDaysInMonth() returns the total number of days in a specific month, for a specific year. The routine must be passed the appropriate month and year.
FloatGetNumDigitsInIntegerPart() returns the number of digits in the integer portion of an FP number. Numbers between zero and one will return one as the number of digits.
FloatStringGetDateNumber(), FloatStringGetTimeNumber()
D.3 Float Formats
FP numbers can be displayed in many ways. For example, as we have seen, an FP number may actually represent a date-time. When we display the FP number 366.0000, we may want to how it (in text) as “Jan 1, 1901.” The Math Library has a number of system-defined formats for your use. You may also allow users to define their own formats with the Float Format controller.
The underlying structures and routines to use and create float format options are explained in the next section. In most cases, however, the simple inclusion of a Float Format controller (of FloatFormatClass) provides all of the UI and functionality to create and apply formats to FP numbers within text objects.
D.3.1 System-defined Formats
A system-defined FP format is stored within a FormatParams structure. This structure defines whether the FP number is a number to be converted into numerical text or a date-time. These format parameters are stored within arrays managed by the format control code.
Code Display D-6 System-defined Float Formats
/*
* System-defined float formats are stored in an array that is maintained and
* accessed by the float controller code. Each element is made up of a
* FormatParams structure.
*/
typedef struct {
/*
* The FloatFloatToAsciiParams_Union stores either a
* FloatFloatToAsciiParams structure if the number is a `pure' FP number,
* or a FloatFloatToDateTimeParams structure if the number is a date-time.
* In this way, it is essentially the same as the FFA_stackFrame discussed
* earlier.
*/
FloatFloatToAsciiParams_Union FP_params;
/*
* FP_formatName stores the name of this formatting option that will be
* displayed in the float controller's dynamic list. This name is loaded
* from the optr given in FP_nameHan and FP_nameOff.(The table where these
* strings are kept is within a localizable resource and therefore will
* have different text under different country setups.)
*/
char FP_formatName[FORMAT_NAME_LENGTH+1];
word FP_nameHan; /* MemHandle */
word FP_nameOff; /* ChunkHandle */
/*
* FP_listEntryNum stores the zero-based position of this FormatParams
* entry within the table.
*/
word FP_listEntryNum;
/*
* FP_signature is an internal field used for error-checking.
*/
word FP_signature;
} FormatParams;
An application will never need to access this table of formats directly. GEOS contains several routines (in math.goh) that can access this table and add, delete and modify table entries. Usually, it is easiest to include a Float Format controller in your application if you intend to allow the user to change float formats with these routines.
There are many system-defined float formatting options. These formats are identified by FormatIdType enumerations. Each type corresponds to a FormatParams structure.
Each FormatIdType enumeration is a direct offset into the float format lookup table. To distinguish between system-defined and user-defined formats, the high bit of a FormatIdType is set to indicate that the format is system-defined. Thus, 8000h refers to the first system-defined format, 8000h + (size(FormatParams)) refers to the second system-defined format, etc.
The format strings themselves are stored within a localizable resource, so that they may appear in a manner relevant to the particular country involved. For example, an FP number of 12.0 using the FormatIdType FORMAT_ID_CURRENCY might appear in the U.S. as $12.00, but will appear as £12.00 in Great Britain.
Code Display D-7 Float Format IDs
typedef enum {
FORMAT_ID_GENERAL = 0x8000,
FORMAT_ID_FIXED = 0x8061,
FORMAT_ID_FIXED_WITH_COMMAS = 0x80c2,
FORMAT_ID_FIXED_INTEGER = 0x8123,
FORMAT_ID_CURRENCY = 0x8184,
FORMAT_ID_CURRENCY_WITH_COMMAS = 0x81e5,
FORMAT_ID_CURRENCY_INTEGER = 0x8246,
FORMAT_ID_PERCENTAGE = 0x82a7,
FORMAT_ID_PERCENTAGE_INTEGER = 0x8308,
FORMAT_ID_THOUSANDS = 0x8369,
FORMAT_ID_MILLIONS = 0x83ca,
FORMAT_ID_SCIENTIFIC = 0x842b,
FORMAT_ID_DATE_LONG = 0x848c,
FORMAT_ID_DATE_LONG_CONDENSED = 0x84ed,
FORMAT_ID_DATE_LONG_NO_WKDAY = 0x854e,
FORMAT_ID_DATE_LONG_NO_WKDAY_CONDENSED = 0x85af,
FORMAT_ID_DATE_SHORT = 0x8610,
FORMAT_ID_DATE_SHORT_ZERO_PADDED = 0x8671,
FORMAT_ID_DATE_LONG_MD = 0x86d2,
FORMAT_ID_DATE_LONG_MD_NO_WKDAY = 0x8733,
FORMAT_ID_DATE_SHORT_MD = 0x8794,
FORMAT_ID_DATE_LONG_MY = 0x87f5,
FORMAT_ID_DATE_SHORT_MY = 0x8856,
FORMAT_ID_DATE_YEAR = 0x88b7,
FORMAT_ID_DATE_MONTH = 0x8918,
FORMAT_ID_DATE_DAY = 0x8979,
FORMAT_ID_DATE_WEEKDAY = 0x89da,
FORMAT_ID_TIME_HMS = 0x8a3b,
FORMAT_ID_TIME_HM = 0x8a9c,
FORMAT_ID_TIME_H = 0x8afd,
FORMAT_ID_TIME_MS = 0x8b5e,
FORMAT_ID_TIME_HMS_24HR = 0x8bbf,
FORMAT_ID_TIME_HM_24HR = 0x8c20,
FORMAT_ID_INDETERMINATE = 0xffff
} FormatIdType;
D.3.2 User-defined Formats
Users may also design their own float formatting options. These user-defined formats are stored in FormatEntry structures. The array of these user-defined formats is kept separate from the system-defined formats. (user-defined formats are stored within their own VM block).
User-defined FormatIdType enums do not have the high bit (8000h) set in order to distinguish them from system-defined FormatIdType enums.
Code Display D-8 User-defined Formats
/*
* User-defined formats are stored in a VM block that is created and maintained by
* the float controller code. As each new format is added, space is made for a
* FormatEntry structure. As formats are deleted, their entry's FE_used field is
* set to zero to indicate that the entry is free for new formats to overwrite.
*/
typedef struct {
/*
* Each FormatEntry contains a corresponding FormatParams structure.
*/
FormatParams FE_params;
/*
* FE_listEntryNumber is the zero-based position of the format counting
* both previous user-defined formats and system-defined formats. For
* example, if there are 10 system-defined formats, the first user-defined
* format will have a FE_listEntryNumber of 10 (because positions are
* zero-based).
*/
word FE_listEntryNumber;
/*
* FE_used, if non-zero, indicates that this entry within the user-defined
* list is currently in use. If FE_used is zero, then this entry position
* may be used to add a new user-defined entry without increasing the size
* of the VM block.
*/
byte FE_used;
/*
* FE_sig is an error-checking field used internally.
*/
word FE_sig;
} FormatEntry;
D.4 Direct FP Operations
The Math Library allows your application to use floating point (FP) numbers. C Developers will find little reason to make direct calls to functions in the Math Library as most of this functionality is taken care of for you in the C environment. (An exception is conversions from FP numbers to ASCII text characters and use of special date-time routines.) Assembly developers, however, will find direct use of the functions and structures in the Math Library essential.
The latter half of this chapter (from this point on) is provided for Assembly developers who need more complete information about the intricacies of the Math Library. Much of this information may also be useful for C developers who wish to make direct calls to the functions in this library for optimization purposes.
D.4.1 Floating Point Numbers
The Math Library defines floating point numbers by using binary point representation. In this format the bit in the zeros place is multiplied by 20, the bit in the minus-ones place is multiplied by 2-1, etc. The exponent is in base 2. For example, the Binary Point representation for 5 is:.
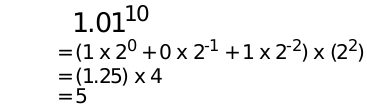
Figure D-1 Translating FP to decimal
Binary Point Representation for the number five, translated
Floating Point Numbers in GEOS follow the IEEE 754 standard used by Intel. In this format a floating point number is represented in an 80 bit (5 word) format. (In C, this type is known as a long double.) This format specifies that the 80 bits contain:
- a 1 bit sign (the most significant bit).
- a 15 bit exponent (0000h to 7FFFh).
- a 64 bit mantissa.
The 15 bit exponent is biased by 3FFFh, so that an exponent of 1 would be represented by 4000h, and an exponent of -1 would be represented by 3FFEh. This produces a hexadecimal range for the exponent of 4000h, or a decimal range of ±4932.
Infinity is represented by 7FFFh in the exponent and 1 followed by 63 zeros in the mantissa. Therefore, all exponent bits are set to 1. (Negative infinity is the same except that the sign bit is also set to 1).
Zero is a special case in which all 80 bits- sign, exponent, and mantissa-are set to zero.
The mantissa is normalized so that the most significant bit is always 1 (except when the FP number is zero). The binary point follows this 1 bit. This produces a precision of approximately 19 decimal places, which is adequate for most needs. This most significant bit is not “assumed away”; it is always present in the mantissa.
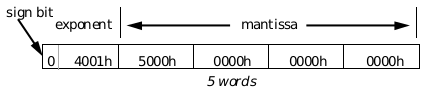
Figure D-2 Diagram of an 80-bit Floating Point Number
Here we see 5( 1.25 x 22) represented as a floating point number.
Note that in most uses, the use of binary point representation is transparent to the application.
D.4.2 The Floating Point Stack
Floating Point (FP) numbers are placed and manipulated on an FP stack. Numbers can be rearranged, operated on, and removed from this stack through pushes, pops, and the use of special routines.
D.4.2.1 Initialization of the FP Stack
FloatInit(), FloatExit()
Before performing any floating point operations, a thread needs to call FloatInit() to create and initialize an FP stack. Each thread using floats must have its own unique FP stack. This call to FloatInit() is automatically performed by any application that includes the Math Library.
FloatInit() creates a swapable block of memory for the thread, initializes various stack pointers, and stores the handle for the block in the thread’s data structure. FloatInit() must be passed the size of the stack to create (in bytes) and the type of stack (FloatStackType) to create.
The default FP stack holds 25 FP elements (250 bytes). An FP stack must be able to hold at least 5 FP elements.
The default floating point stack is FLOAT_STACK_GROW which instructs the system to increase the size of the stack whenever its bounds are reached. This is done automatically.
Other FloatStackType types are FLOAT_STACK_WRAP, which drops the FP numbers at the low end of the stack (effectively wrapping over that end) and FLOAT_STACK_ERROR which signals an error when the stack limit has been reached.
FloatExit() detaches the floating point stack for the current thread and frees its memory. FloatExit() only frees the FP stack associated with the current thread; other FP stacks in other threads remain unaffected. As is the case with FloatInit(), the call to FloatExit() is automatically performed by any application that includes the Math Library.
If FloatInit() is called twice before calling FloatExit(), the data on the original floating point stack will be lost.
D.4.2.2 Pushing and Popping on the FP Stack
FloatPushNumber(), FloatPopNumber(), FloatDepth()
FloatPushNumber() pushes an FP number onto the top of the FP stack for the current thread from a passed buffer. The number must be already set up in 80 bit, FP format. The routine must be passed the pointer to the buffer storing the number.
Similarly, FloatPopNumber() pops an FP number from the top of the FP stack for the current thread into a passed buffer.
FloatDepth() returns the number of FP numbers currently in place on the stack.
Note: For clarity in diagrams within this chapter, stack locations will be numbered in order from the top position of the stack, S1 being first, S2 being second, etc. Variables will be numbered in the order they are pushed onto the stack, so that if X1, X2, and X3 are pushed onto the stack, the format in Figure D-3 will result.

Figure D-3 The Floating Point Stack
D.4.2.3 FP Stack Manipulation
FloatRoll(), FloatRollDown(), FloatRot(), FloatSwap()
Besides basic pushing and popping, the Float Library also includes many other routines which manage FP numbers on the stack. Unless otherwise specified, an operation that pushes, pops, or extracts an FP number on the stack affects all other FP numbers below the position of the operation by shifting their location in the stack either up or down, in standard stack fashion.
FloatRoll() pushes a selected FP number (SX) onto the top of the stack (S1), removing it from location SX in the process. FloatRoll() passed with a value of 3 would move the FP number in S3 onto the top of the stack, pushing the stack in the process. All FP numbers below the extracted number remain unaffected by this routine.
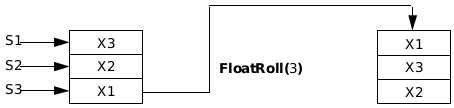
FloatRollDown() performs the inverse operation of FloatRoll(). popping the top stack value (S1) into the specified location on the stack (SX). FloatRollDown() passed with a value of 3 would move the FP number in S1 into location S3, shifting the stack in the process.

Both of these routines must be passed a stack location to move to or from.
FloatRot() rotates the top three numbers on the stack, placing S3 onto the top of the stack. This is equivalent to a FloatRoll() passed with a value of 3.
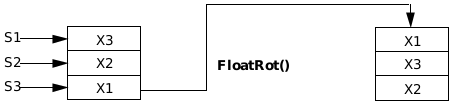
FloatSwap() exchanges S1 and S2.

Repetitious applications of these routines will return the stack to its former state.
D.4.2.4 Copying and Deleting Numbers on the FP Stack
FloatPick(), FloatOver(), FloatDrop(), FloatDup()
FloatPick() copies the contents of SX and pushes that value onto the FP stack. The entire stack is pushed in the process. FloatPick() passed with a value of 3 would copy the contents of S3 onto the FP stack.
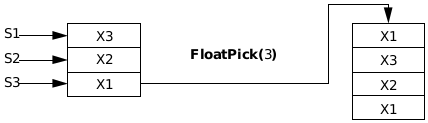
FloatOver() copies S2 to the top of the stack, equivalent to a FloatPick() passed with a value of 2.
FloatDrop() drops (pops) the top number (S1) off the FP stack. This routine is different than FloatPopNumber() because the routine does not place the popped number into a memory address, and is therefore much faster.

FloatDup() duplicates the value at S1, pushing it onto the top of the stack. The stack is pushed in the process.

D.4.2.5 Comparing Numbers on the FP Stack
FloatComp(), FloatCompESDI(), FloatCompAndDrop()
These routines essentially perform the same operation as the Assembly command cmp. FloatComp() performs a compare of the top two FP numbers (S1 and S2) and sets the appropriate flags in the flags register. The two FP numbers remain on the stack. FloatCompESDI() compares the contents of es:[di] with the value in S1 (and the FP number in S1 remains on the stack). FloatCompAndDrop() performs a compare of S1 and S2 and drops both from the FP stack.
D.4.2.6 Recovery of the FP Stack
FloatGetStackPointer(), FloatSetStackPointer()
FloatGetStackPointer() returns the current stack pointer value of the FP stack. FloatSetStackPointer() sets the stack pointer to a previous position. This routine must be passed a value that is greater than or equal to the current value of the stack pointer. (I.e. you must be throwing something, or nothing, away.)
These routines may be useful before the execution of involved routines that may push many numbers onto the stack. If an unrecoverable error is encountered, the programmer need not pop the intermediate values off the stack to return to the previous stack configuration. Only the stack pointer is saved; the state of the stack is not. If any numbers below the stack pointer are popped or altered, FloatSetStackPointer() will not recover the previous state of the stack.
D.4.3 Floating Point Math Routines
The Float Library provides a number of routines to modify data on the FP stack. These routines can be categorized in several major groups:
- Constant Routines
- Math Routines
- Transcendental Routines
- Conversion Routines
- Date and Time Routines
D.4.3.1 Constant Routines
Float0(), FloatPoint5(), Float1(), FloatMinusPoint5(), FloatMinus1(),Float2(), Float5(), Float10(), Float3600(), Float16384(), Float86400()
FloatPi(), FloatPiDiv2(),FloatLg10(), FloatLn2(), FloatLn10(), FloatSqrt2()
The Constant Routines provide a means of quickly obtaining an often used number or an often used operation with a constant operand. Each of these functions pushes the constant FP value onto the top of the FP stack. (For example, FloatMinusPoint5() pushes -.5 onto the FP stack.)
FloatPi(), FloatPiDiv2(), FloatLg10(), FloatLn2(), FloatLn10(), and FloatSqrt2() each push the specified transcendental constant onto the FP stack: π,π/2, the log of 10, the natural log of 2, the natural log of 10,and the square root of 2, respectively. (See also Transcendental Routines.)
D.4.3.2 Constant Operands
FloatMultiply2(), FloatMultiply10(), FloatDivide2(), FloatDivide10(), Float10ToTheX()
FloatMultiply2(), FloatMultiply10(), FloatDivide2(), FloatDivide10() perform the specified operations on the contents of S1, either multiplying or dividing the contents of S1 by 2 or 10, and push the result onto the FP stack. The original value in S1 is popped off of the stack.
Float10ToTheX() pushes 10 to a passed exponent onto the FP stack.
D.4.3.3 Algebraic Routines
FloatAbs(), FloatAdd(), FloatSub(), FloatDivide(), FloatMultiply(), FloatDIV(), FloatMod(),FloatFactorial(), FloatNegate(), FloatInverse()
The Math Routines perform various operations on numbers already placed on the FP stack. All of the following routines pop the operated numbers off of the stack and push the result onto S1.
FloatAdd() adds the contents of S1 and S2, and pushes the result onto the top of the FP stack. The original values are popped off the stack.
FloatSub() subtracts the contents of S1 from the contents of S2, and pushes the result onto the top of the FP stack. The original values are popped off the stack.
Note that, in general, numbers will be pushed onto the stack in the order they would normally be operated on. For example, to obtain X1-X2, the programmer would first push X1, then X2, and call FloatSub, as in the following diagram:
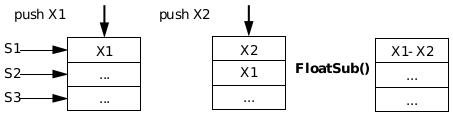
since X1 would now be in location S2, while X2 is in location S1.
FloatMultiply() multiplies the contents of S1 and S2 and pushes the result onto the top of the FP stack. The original values are popped off the stack.
FloatDivide() divides the contents of S2 by the contents of S1 and pushes the result onto the top of the FP stack. The original values are popped off the stack.
FloatDIV() performs a FloatDivide(), truncating the fractional portion of the number and returning only the integer result. The original values are popped off the stack.
FloatMod() pushes S2 mod S1 (the remainder of FloatDivide()) onto the top of the FP stack. The original values are popped off the stack.
FloatAbs() pushes the absolute value of S1 onto the top of the FP stack. The original value is popped off the stack.
FloatFactorial() pushes the factorial (x!) of the value in S1 onto the top of the FP stack. The original value is popped off the stack.
FloatNegate() negates the value in S1 and pushes the result onto the top of the FP stack. The original value is popped off the stack.
FloatInverse() pushes the inverse of the value in S1 (-S1) onto the top of the FP stack. The original value is popped off of the stack.
D.4.3.4 Comparison Routines
FloatMax(), FloatMin(), FloatLt0(), FloatEq0(), FloatGt0()
FloatMax() performs a compare of the FP numbers in S1 and S2 and, if necessary, swaps the greater number into S1.
FloatMin() performs a compare of the FP numbers in S1 and S2 and, if necessary, swaps the lesser number into S1.
FloatLt0(), FloatEq0(), FloatGt0() check whether the FP number in S1 is less than zero, equal to zero, or greater than zero. The carry bit is set to TRUE if the relationship is true. The original value is popped off of the stack.
D.4.3.5 Fractional and Integral Routines
FloatFrac(), FloatTrunc(), FloatInt(), FloatIntFrac(), FloatRound()
FloatFrac() pushes the fractional portion of S1 onto the FP stack. The original value is popped off of the stack.
FloatTrunc() pushes the integral portion of the contents of S1 onto the FP stack. This amounts to a rounding of the FP number toward zero, so that FloatTrunc() performed on -7.8 would return -7. The original value is popped off the stack.
FloatInt() rounds S1 down to its integral component, so that FloatInt() performed on -7.8 would return -8. Note that for negative numbers, this is different from FloatTrunc(). The original value is popped off the stack.
FloatIntFrac() splits a number into its fractional and integral parts, with the fractional part in S1 and the integral part in S2. The original value is popped off the stack.
FloatRound() rounds S1 to a given number of decimal places. FloatRound() passed with zero as an argument rounds S1 to the nearest integer, rounding up if greater than or equal to .5, rounding down if less than .5
D.4.3.6 Routines that Return Random Values
FloatRandom(), FloatRandomN(), FloatRandomize()
FloatRandom() pushes a random number between 0 (inclusive) and 1 (exclusive) onto the stack.
FloatRandomN() pushes a random integer between 0 (inclusive) and N (exclusive) onto the stack.
FloatRandomize() primes the random number generator. This routine expects a seed and some RandomGenInitFlags. If the flag RGIF_USE_SEED is passed, then a developer-supplied seed will be used. Otherwise, a seed based on the timer clock will be used.
FloatRandomize() should always be called before any of the FloatRandom() routines to ensure a high degree of randomness.
The random number generation method uses the linear congruential method, an algorithm which ensures a high degree of randomness in the computation method.
D.4.3.7 Transcendental Functions
Transcendental functions are functions that cannot be constructed using normal arithmetic routines. Care must be taken with the following routines to ensure that they are operating on a valid range of values. Otherwise, the routines will return an error.
Trigonometric Routines
FloatSin(), FloatCos(), FloatTan(), FloatArcSin(), FloatArcCos(), FloatArcTan(), FloatArcTan2(), FloatSinh(), FloatCosh(), FloatTanh(), FloatArcSinh(), FloatArcCosh(), FloatArcTanh()
FloatSin(), FloatCos(), and FloatTan() perform the given operation on the contents of S1, pushing the result onto the FP stack. S1 must be expressed in radians. The original value is popped off of the stack.
FloatArcSin(), FloatArcCos(), and FloatArcTan() perform the given inverse operation on S1, pushing the result onto the FP stack. The result is given in radians. The original value is popped off of the stack.
FloatArcTan2() calculates the arc tangent given cartesian coordinates x and y. The arctangent is calculated from the x-axis through the origin to the given point. The value returned is expressed in radians, between -p (exclusive) and +p (inclusive). The original values are popped off of the stack.
FloatSinh(), FloatCosh(), and FloatTanh() perform the given hyperbolic operations on S1, pushing the result onto the FP stack. The original value is popped off of the stack.
FloatArcSinh(), FloatArcCosh(), and FloatArcTanh() perform the given inverse hyperbolic operations on S1, pushing the result onto the FP stack. The original value is popped off of the stack.
Exponential Routines
FloatExp(), FloatExponential(), FloatLg(), FloatLog(), FloatLn(), FloatLn1plusX(), FloatSqr(), FloatSqrt()
FloatExp() performs the exponentiation of e to the power of S1, pushing the result onto the FP stack. The original value is popped off of the stack.
FloatExponential() performs the exponentiation of S2 to the power of S1, pushing the result onto the FP stack. The original values are popped off of the stack.
FloatLg() performs the logarithm to the base 2 on S1, pushing the result onto the FP stack. The original value is popped off of the stack.
FloatLog() performs the logarithm to the base 10 on S1. The original value is popped off the stack.
FloatLn() performs the natural logarithm (log base e) on S1. The original value is popped off the stack.
loatLn1plusX() performs the natural log of (1 + S1). The original value is popped off the stack.
FloatSqr() performs the square of S1, pushing the result onto the FP stack. The original value is popped off the stack.
FloatSqrt() performs the square root of S1, pushing the result onto the FP stack. The original value is popped off the stack.
D.4.3.8 Conversion Routines
At some point 80-bit FP numbers may need to be converted into different formats, or you may need to convert these differently formatted numbers into a floating point representation. The Math Library provides for this contingency.
Conversions Between Integers and FP Numbers
FloatDwordToFloat(), FloatWordToFloat(), FloatFloatToDword()
FloatDwordToFloat() converts a passed double-word signed integer into a floating point number, and pushes that number onto the FP stack.
FloatWordToFloat() converts a passed word signed integer into a floating point number, and pushes that number onto the FP stack.
FloatFloatToDword() converts the FP number in S1 into a double-word signed integer. The FP number is converted into an integer by rounding the FP number to zero decimal places.
You can convert a FP number into a word value by using FloatFloatToDword() and just using the low word.
Conversions Between 80 bit FP Numbers and Other Floats
FloatGeos80ToIEEE64(), FloatGeos80ToIEEE32(), FloatIEEE64ToGeos80(), FloatIEEE32ToGeos80()
FloatGeos80ToIEEE64() converts a GEOS FP number (80 bits) into a 64 bit floating point number (in C, a type of double).
FloatGeos80ToIEEE32() converts a GEOS FP number (80 bits) into a 32 bit floating point number (in C, a type of float).
FloatIEEE64ToGeos80() converts a 64 bit FP number into a GEOS 80 bit FP number (in C, a type of long double).
FloatIEEE32ToGeos80() converts a 32 bit FP number into a GEOS 80 bit FP number (in C, a type of long double).